| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- PCA #주성분 분석 #머신러닝 #선형대수 #sklearn
- 딥러닝 #머신러닝 #AdaGrad
- 파이썬 #알고리즘 #코딩인터뷰 #리트코드 #DFS
- cyclegan #GAN
- 딥러닝 #모멘텀 #momentum #핸즈온머신러닝 #하이퍼파라미터튜닝
- 3d cad #인공지능 #resnet
- BERT #자연어처리
- 자연어처리 #glove #글로브 #glove vector #벡터 임베딩
- 자연어처리 #기계번역 #attention #global attention # local attention
- 자연어처리 #question-answering #dynamic memory #attention
- 특이값분해 # SVD #머신러닝 #차원축소 # 인공지능
- char-CNN #자연어처리 # 단어임베딩 #wordembedding #LSTM
- 파이썬 #알고리즘 #데크 #원형큐 #코딩테스트
- 배치 정규화 #batch normalization # 딥러닝 #머신러닝
- Today
- Total
누누와데이터
[논문 리뷰] Batch Normalization: Accelerating Deep Network Training by ReducingInternal Covariate Shift 본문
[논문 리뷰] Batch Normalization: Accelerating Deep Network Training by ReducingInternal Covariate Shift
happynunu 2021. 7. 1. 19:471.기존의 Deep Neural Network 정규화 방식의 문제
Neural Network를 안정적으로 잘 학습시키려면, (1) Input 부분에서 정규화 기법을 사용하고 (2)각 층의 weight를 √(n/2) 로 나누어 표준화를 진행한다.
하지만 Layer가 깊어질수록 input 부분에서 정규화한 효과가 없어진다(내부 공변량 변화 : Internal Covariate Shift)
이전 파라미터들이 업데이트 됨에 따라 다음에 번에 있는 Hidden Layer들의 입력 분포가 변경 됩니다. 이는 Layer가 깊을수록 심화될 수 있습니다.
2.Internal Covariate Shift

Internal Covariate Shift(내부 공변량 변환)는 학습 도중 신경망 파라미터 변화에 의해서 발생되는 신경망 activation 분포의 변화입니다. 이러한 내부 공변량 변환 문제는 (1) ReLU 함수를 이용하거나 (2) 신중한 초기값 선택, (3)적은 학습률을 적용하여 문제를 해결할 수 있습니다. 하지만 (1) ReLU함수를 적용한다고 해도, 훈련 초기 단계에서는 괜찮지만 훈련 중 후반부로 가면서 똑같은 문제가 발생할 수 있으며, (2) 적절한 초기값을 이용하는 것은 어려운 일이고, (3)적은 학습률을 적용하게 되면 학습 속도가 느려지게 되는 문제가 있습니다.
3.1 Batch Normalization 공식과 적용
논문에서는 Internal Covariate Shift의 문제를 해결하여 Neural Network의 성능을 높이고자 하였습니다.
Batch Normalization 방법은 초기 입력 레이어만 정규화 했던 과거의 방식을 확장시켜서 모든 Hidden layers 각각에 data가 input를 하기 전에 정규화를 적용하는 것입니다.

일반적으로 배치 정규화는 아래의 그림과 같이 Fully Connected(FC)나 Convolutional layer 바로 다음, 활성화 함수를 통과하기 전에 배치 정규화(BN)레이어를 삽입하여 사용한다.
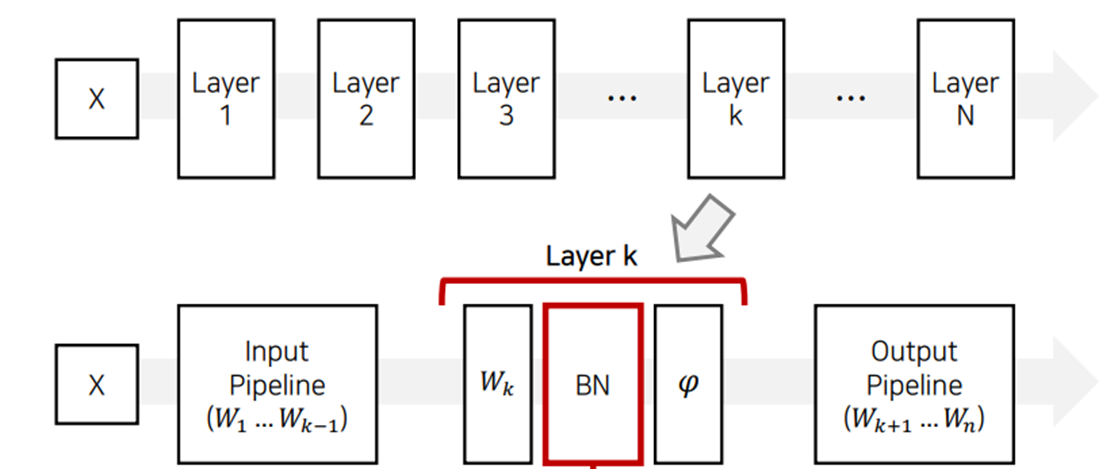
3.2 Batch Normalization에 scale, shift 연산이 필요한 이유
입력값은 x1, x2, ...xm까지 있는 mini batch이고 size는 m이다. 학습되는 파라미터는 감마(gamma)와 베타(Beta)이다.
레이어의 입력 차원이 m 일때, 학습할 두개의 파라미터 감마(gamma)와 베타(Beta) 또한 m 차원을 가진다.
공식을 보면, 입력데이터를 normalize하고 이러한 데이터에 scale과 shift 연산을 취하는 것을 알 수 있다. 𝛾가 scale 연산을 하고 𝛽가 shift 연산을 한다. 𝛾와 𝛽는 학습이 될 때, backpropagation과 확률적 경사 하강법을 통해서 학습이 된다. 𝛾는 1로 초기화를 진행하고, 𝛽는 0으 로 초기화를 진행한다.

scale과 shift 연산이 필요한 이유는 각 layer를 단순히 N(0,1)로 정규화되면 대부분의 입력에 대해 매우 선형적으로 동작하므로, 기존의 비선형 함수의 영향력이 사라지기 때문입니다. 예를 들어, 위의 sigmoid 함수 그래프를 보면, 0을 기점으로해서 데이터가 분포하는 정규 분포는 sigmoid 함수에 대입했을 때, 선형적인 구간에만 주로 분포가 될 것 임을 알 수 있다.
3.3 Batch Normalization의 이동 평균 적용

training시에는 mini-batch의 평균과 표준편차를 계산해 batch normalization를 수행하지만, test시에 batch normalization를 적용할 때는 훈련하는 동안 구한 layer에서의 입력평균과 표준편차 각각의 이동 평균을(moving average) 구해서 이에 대한 최종 통계를 추정한다.
+ 이동평균은 학습시에 각 mini-batch마다 구한 입력평균과 입력 표준편차 값을 구하고 저장한 뒤에, 저장된 입력평균과 입력 표준편차의 평균을 각각 구해서 테스트시에 사용합니다.
4. Batch Normalization 성능 향상

참고 및 출처
논문 : https://arxiv.org/abs/1502.03167v3
출처 : 배치 정규화(Batch Normalization) [꼼꼼한 딥러닝 논문 리뷰와 코드 실습] https://www.youtube.com/watch?v=58fuWVu5DVU


